Any number that can be expressed in the form p upon q is called a rational number. For example: upon upon -upon etc. And the simple way to think about it is any number that can be represented as the ratio of two integers is a rational number.
So for example, any integer is a rational number. Number lines have many uses both in mathematics and everyday life. This lesson will teach you how to graph numbers on a number line and give real-world examples of how to use number lines.
A Rational Number can be written as a Ratio of two integers (ie a simple fraction). An integer is a number with no fractional part. A number that can be made by dividing two integers.
The word comes from ratio. But (pi) is not a rational number , it is an Irrational Number. Rational numbers are any numbers that can be written as a fraction. In other words, you can rewrite the number so it will have a numerator and a denominator.
Notice that we said b cannot be zero. Now, why are and examples of such numbers ? We can also write rational numbers as a decimals. If an unlimited precision integer type is available, rational numbers based on it will never overflow and will provide exact calculations in all circumstances.
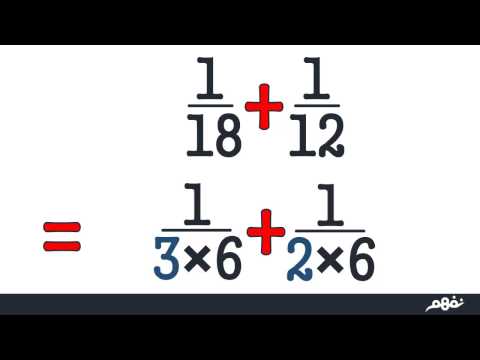
Integer Type Requirements. The rational type takes a single template type. Learn vocabulary quiz math integers rational numbers algebra with free interactive flashcards.
Choose from 5different sets of vocabulary quiz math integers rational numbers algebra flashcards on Quizlet. Since q may be equal to every integer is a rational number. Rational Numbers Unit Test: The test consists of multiple choice questions, utilizing Mastery Connect. Many numbers are rational. By definition of rational , all fractions are rational numbers.

That would take an infinite amount of time - an well, infinity is not a rational number. This concept is distinct from that of a real number, which can take on many more values (for example, the square root of which cannot be represented as a fraction). All rational numbers belong to the real numbers.
If you look at a numeral line. You notice that all integers, as well as all rational numbers , are at a specific distance from 0. Classifying rational numbers is such a tricky skill for m My 7th grade math students loved this activity! Explore rational functions interactively using the links below.
An app to Rational Functions and Their Asymptotes There is also another app to explore Rational Functions and Their Transforms. They use the number line model to support their understanding of the rational numbers and the number system. The number system is revisited at the end of the year (in Module 7) to develop the real number line through a detailed study of irrational numbers.
No comments:
Post a Comment
Note: only a member of this blog may post a comment.